L’importanza del modello dinamico di una struttura
Un esempio semplice per comprendere l’importanza del modello dinamico delle strutture

Dinamica delle strutture
La dinamica delle strutture pone le basi per lo studio dell’ingegneria sismica.
Quando si parla di dinamica delle strutture la prima cosa che viene in mente ad un progettista strutturale è l’oscillatore semplice.
L’oscillatore semplice è un modello dinamico.
Qual è però l’importanza del modello dinamico di una struttura? Come si lega il modello dinamico di una struttura con il modello dell’oscillatore semplice se la totalità delle strutture progettate non si comporta come tale?
L’oscillatore semplice definisce un sistema con un solo grado di libertà dal punto di vista dinamico.
Una struttura con un solo grado di libertà dal punto di vista dinamico è una struttura la cui generica configurazione deformata è governata da un solo parametro.
Si può, in via approssimata, considerare un portale formato da un traverso e due piedritti come una struttura con un solo grado di libertà e, quindi, come un oscillatore semplice.
Possiamo, infatti, ipotizzare la massa di questo sistema concentrata nel traverso e studiare il suo comportamento dinamico considerando gli spostamenti orizzontali della massa concentrata.
Nessuna struttura però, nella realtà, si comporta come un oscillatore semplice. Tutte le strutture, anche le più semplici, dal punto di vista dinamico, sono governate da molti parametri.
La scelta del modello dinamico di una struttura, però, non dipende solo dal numero di parametri che governano la sua configurazione deformata, ma anche dal problema che si vuole studiare.
Se noi consideriamo il portale precedentemente descritto e vogliamo studiare di esso sia il comportamento dinamico nella direzione orizzontale che quello nella direzione verticale non possiamo utilizzare lo stesso modello dinamico.
Possiamo innanzitutto semplificare il problema dicendo che la massa del traverso è molto più grande di quella dei piedritti. Per tale motivo la massa del sistema si viene a concentrare nel traverso.
Inoltre la rigidezza estensionale del traverso (EA) è molto più elevata della rigidezza flessionale dei piedritti.
Queste due ipotesi ci permettono di semplificare il portale, dal punto di vista dinamico, con una massa concentrata nel traverso, e studiare, di conseguenza, il suo comportamento dinamico considerando solo gli spostamenti della massa nella direzione orizzontale.
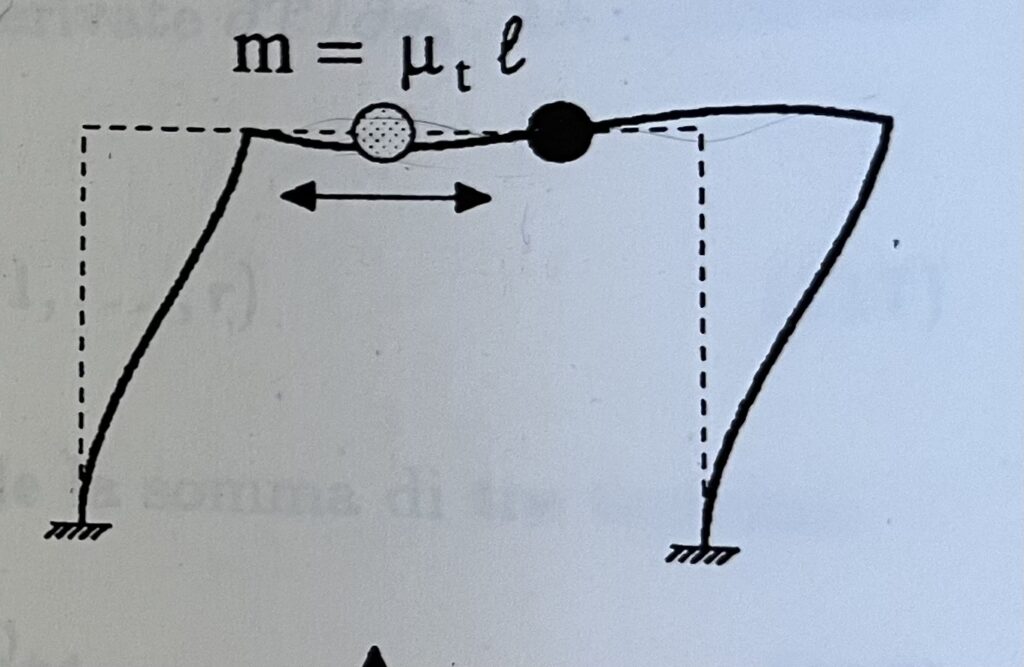
Fonte “Dinamica delle strutture” di Roberto Ramasco
Se invece volessimo studiare il comportamento dinamico della struttura nella direzione verticale, la semplificazione adottata per il caso precedente non andrebbe bene e comporterebbe la perdita di molte informazioni comportamentali della struttura stessa.
In questo caso, la rigidezza estensionale dei piedritti rispetto a quella flessionale del traverso, implica che esso si comporti come una trave elasticamente incastrata agli estremi.
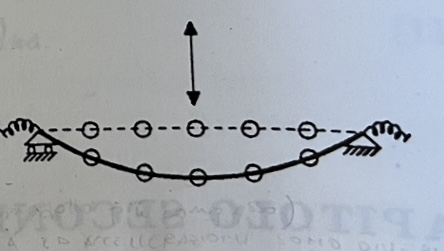
Fonte “Dinamica delle strutture” di Roberto Ramasco
Ipotizzare quindi la presenza di una sola massa concentrata nel traverso non è sufficiente per studiare il suo comportamento dinamico nella direzione verticale.
Ѐ necessario discretizzare la massa concentrata in più parti ottenendo, in questo modo, un sistema con un numero di gradi di libertà pari al numero di masse ipotizzate.
Così facendo si possono studiare in maniera precisa le oscillazioni verticali del sistema, senza perdere informazioni in merito al suo comportamento dinamico.
In questo modo si dimostra quindi che il modello dinamico di una struttura non è solo in funzione della sua generica configurazione deformata, ma è anche in funzione dello studio che di tale struttura si intende fare.
Leggi anche Effetti dello smorzamento proporzionale nella risposta dinamica strutturale

Codice degli appalti: il Cdm approva il testo


Gli utilizzi delle barre in materiale composito fibro-rinforzato