Gli albori del FEM e l’elemento triangolare lineare
Il metodo degli elementi finiti (FEM) è stato sviluppato da diversi ricercatori nel corso degli anni, con contributi significativi provenienti da diversi campi della scienza e dell’ingegneria.
ll concetto di base ha le sue radici nel XIX secolo, quando matematici come Gauss, Ritz, Rayleigh e Galerkin iniziarono a sviluppare metodi approssimativi per risolvere equazioni differenziali alle derivate parziali. Tuttavia, il vero sviluppo del metodo degli elementi finiti ha avuto luogo negli anni ’50 e ’60 del XX secolo.
Uno dei primi sviluppatori del metodo fu A. Hrennikoff, un ingegnere strutturista russo-canadese, che nel 1941 pubblicò un lavoro in cui proponeva un metodo per risolvere numericamente le equazioni differenziali che descrivono il comportamento di una struttura elastica mediante l’uso di un grigliato di barre.
Due anni dopo R. Courant dimostrò che, scomponendo un dominio continuo in una serie di triangoli e approssimando le soluzioni all’interno di ciascun triangolo con funzioni lineari, era possibile ottenere una soluzione ai problemi espressi da equazioni differenziali alle derivate parziali del secondo ordine. Questa metodologia sfruttava i vantaggi delle tecniche variazionali sviluppate da Ritz e Galerkin, fornendo un approccio sistematico per la discretizzazione e la risoluzione delle equazioni alle derivate parziali.
La proposta di Courant non ebbe impatto sulla comunità di strutturisti e dovettero passare altri dieci anni perché l’idea attirasse l’attenzione degli ingegneri che la riscoprirono e la svilupparono come un metodo per l’analisi strutturale. Nel 1952, l’allora giovane ricercatore della Università di Berkeley, R. W. Clough, fece domanda per partecipare ad una attività di ricerca promossa dalla Boeing e, collaborando con M. J. Turner, un ingegnere della Boeing Aircraft Company, sviluppò un metodo simile a quello di Courant.
J. H. Argyris, che lavorava presso l’Imperial College di Londra, ebbe un ruolo chiave nello sviluppo del metodo fin dalle sue origini. Infatti, ricevette i rapporti dal gruppo di lavoro della Boeing e integrò il materiale in un suo fondamentale articolo sull’utilizzo dei metodi energetici nell’analisi strutturale, pubblicato a metà di quel decennio. Il lavoro di Argyris fu di ispirazione per Turner e Claugh che lo utilizzarono per formalizzare il loro lavoro di ricerca. I loro risultati furono finalmente pubblicati sugli atti dell’Institute of Aeronautical Sciences e poi sul Journal of Aerospace Science nel 1956.
Fino alla fine del decennio, Clough e i suoi collaboratori di Berkeley portarono avanti l’idea e l’applicarono eseguendo calcoli manuali prevalentemente utilizzati in ambito civile. Solo nel ’60, E. L. Wilson, un altro studente di Clough, decise di implementare il metodo in FORTRAN. Così nacque il primo software per risolvere problemi in stato piano di tensione o di deformazione mediante l’attuale metodo degli elementi finiti. Il software di Wilson, un predecessore dell’attuale SAP, utilizzava una discretizzazione arbitraria di elementi triangolari su cui veniva considerata una deformazione costante. In quello stesso anno Clough presentò un lavoro ad una conferenza dedicata al calcolo elettronico organizzata dall’American Society of Civil Engineers. In quel lavoro Clough battezzò il metodo col nome attuale.
Quando Clough presentò il primo articolo sul metodo degli elementi finiti nel 1960, attirò l’attenzione del suo collega e amico, O. C. Zienkiewicz, allora docente alla Northwestern University. Zienkiewicz era già esperto di fama mondiale nell’applicazione del metodo delle differenze finite alla meccanica dei continui in ingegneria civile, ma, dopo quell’incontro, divenne un sostenitore del metodo degli elementi finiti, tanto da diventarne uno dei massimi esperti mondiali. Infatti, si deve a lui e al suo collaboratore B. M. Irons la paternità, nel 1968, dell’approccio isoparametrico. Questo metodo consente di descrivere la geometria degli elementi finiti utilizzando le stesse funzioni di interpolazione impiegate per il campo di spostamenti.
Quella descritta in questo articolo è una versione rivista in chiave moderna dell’elemento triangolare lineare inizialmente proposto da Turner e Clough, riformulato prendendo vantaggio dall’utilizzo dell’approccio isoparametrico, e dall’utilizzo di un particolare sistema di coordinate specifico per gli elementi triangolari. Questo sistema di coordinate è denominato, appunto, sistema di coordinate triangolari. L’idea di utilizzarlo nelle formulazioni di elementi triangolari fu proprio di Argyris, lo stesso che, dieci anni prima, ispirò il lavoro di Turner e Clough alla Boeing.
L’elemento triangolare lineare
Per la sua valenza storica e didattica, e grazie alla sua semplicità, l’elemento triangolare lineare è una delle prime formulazione che si studia nei corsi universitari sul metodo degli elementi finiti. L’elemento è costituito da un triangolo piano con tre nodi, posizionati nei vertici del triangolo. Ogni nodo ha due gradi di libertà, che corrispondono agli spostamenti del nodo lungo le direzioni x e y, come mostrato in Figura 1(A).
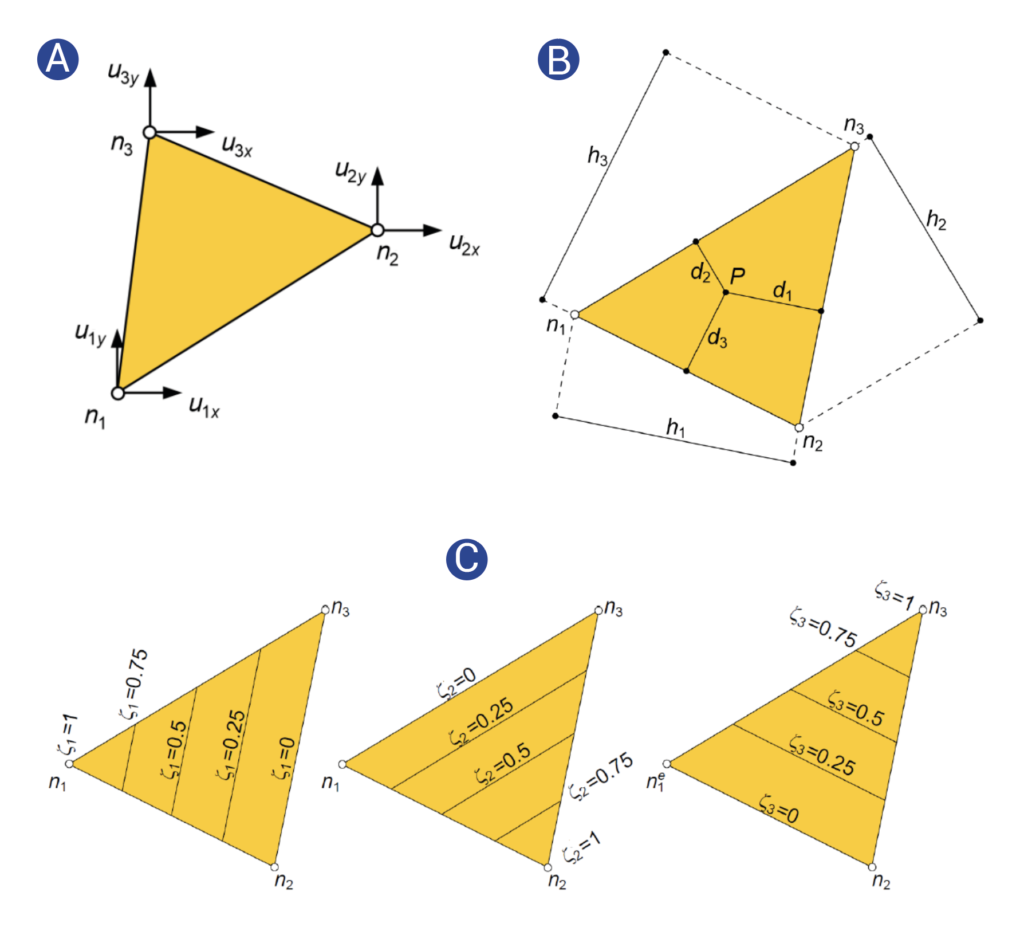
>> Figura 1 L’elemento triangolare lineare: (A) nodi e gradi dilibertà, (B) grandezze necessarie a definire le coordinate triangolari di un punto, (C) sistema di coordinate triangolari.
Le coordinate triangolari
Per descrivere la geometria di un elemento triangolare, è utile utilizzare un sistema di coordinate specifico per i triangoli. Le coordinate triangolari esprimono la posizione di un punto P all’interno del triangolo in funzione della distanza di P dai lati del triangolo stesso.
Riferendoci alla Figura 1(B), indichiamo con di la distanza di P dal lato Li, che è opposto al vertice ni. Il valore massimo che di può raggiungere è l’altezza hi del triangolo rispetto alla base Li. La coordinata ζi di P è definita come il rapporto ζi = di/hi.
Secondo questa definizione, ogni punto P ha tre coordinate, calcolate prendendo come base ciascuno dei tre lati del triangolo. Il valore massimo che ciascuna coordinata può assumere è 1, che si verifica quando il punto coincide con un vertice del triangolo. Naturalmente, non può accadere che tutte le coordinate ζ1, ζ2e ζ3 siano pari a 1 contemporaneamente. Ad esempio, se ζ2=1, significa che P coincide con il vertice n2 e quindi sarà sui lati L1 e L3, implicando che ζ1 e ζ3 saranno entrambe pari a 0. In generale, per qualsiasi punto P, la somma delle tre coordinate sarà sempre uguale a 1, cioè
ζ1 + ζ2+ ζ3 = 1
Nella Figura 1(C) sono rappresentate le linee lungo cui ciascuna delle tre coordinate triangolari rimane costante. Queste linee sono parallele a uno dei lati del triangolo perché dipendono dalla distanza del punto da quel lato. Queste linee parallele ci aiutano a visualizzare come cambia la posizione di un punto all’interno del triangolo in base alle coordinate triangolari.
Un esempio significativo è il centro del triangolo, noto anche come baricentro. Questo punto ha coordinate triangolari ζ1 = ζ2= ζ3 = 1/3. Questo perché il baricentro di un triangolo si trova a un terzo della distanza dalla base rispetto all’altezza. Poiché ci sono tre lati e quindi tre altezze possibili, il baricentro ha uguale distanza proporzionale da ciascuno dei lati, risultando in proporzione di 1/3 per ciascuna delle tre coordinate triangolari.
Un altro punto significativo del triangolo è il punto medio di ciascuno dei tre lati. Le coordinate di questi punti sono tali che la coordinata ζi del punto medio del lato Li è zero, mentre le altre due coordinate sono pari a 1/2. Questo perché il punto medio è equidistante dagli altri due lati del triangolo.
Infine, consideriamo come ulteriore esempio quello relativo ai vertici del triangolo. In questi punti, due delle coordinate sono zero e una è pari a uno. Questo accade perché un vertice si trova all’intersezione di due lati del triangolo; quindi, la distanza da questi lati è zero, mentre la coordinata rimanente, che rappresenta la distanza del vertice dal lato opposto, è uguale all’altezza del triangolo rispetto a quella base. In altre parole, se siamo sul vertice opposto al lato Li, la coordinata ζi sarà 1, mentre le altre due coordinate saranno 0.
Per leggere l’articolo completo acquista il numero 19 della rivista Lo Strutturista.
Per essere sempre aggiornato e leggere contenuti inediti abbonati alla rivista Lo Strutturista – La prima rivista per gli strutturisti italiani.

Corso di alta formazione in diagnosi, intervento e recupero di strutture esistenti in muratura

Convegno “Novità dal settore delle costruzioni e obbligatorietà del BIM”

Al SED di Caserta l’incontro con gli autori de “Lo Strutturista” a cinque anni dalla nascita.

ISAAC – Electro-Pro


Corso di alta formazione in diagnosi, intervento e recupero di strutture esistenti in muratura