Blumatica - Software edilizia e sicurezza

Carico critico elastico e snellezza limite

Approfondimento sul problema dell’instabilità dei profili in acciaio a cura di Blumatica.

23 Luglio 2020

Blumatica - Software edilizia e sicurezza

Le prime trattazioni riguardanti il problema dell’instabilità risalgono al XVIII secolo con Eulero che, ispirato dagli studi sulla linea elastica di Bernoulli, diede vita alla formulazione del carico critico elastico. Attualmente questo è definito nel seguente modo:

$N_{cr}=\pi^{2}EI/l_{0}^{2}$

In cui:

E Modulo elastico del materiale costituente la sezione;
I Inerzia della sezione trasversale;
l₀=μ*l Lunghezza libera di inflessione;
l Lunghezza dell’asta vincolata;
Coefficiente di vincolo.

L’instabilità è correlata dunque alla lunghezza libera di inflessione, distanza tra due punti di flesso della configurazione deformata di un’asta, ed alle condizioni di vincolo, secondo il coefficiente μ:

μ=1 Trave vincolata con 2 cerniere agli estremi;
μ=2 Trave vincolata con un solo incastro perfetto (mensola);
μ=0,5 Trave vincolata con 2 incastri perfetti agli estremi;
μ=v0,7 Trave vincolata con un incastro perfetto e una cerniera.

La tensione critica, ovvero quella che si sviluppa in corrispondenza del carico critico N_cr, è data da:

$\sigma_{cr}=\frac{N_{cr}}{A}=\frac{\pi^{2}EI}{Al_{0}^{2}}=\frac{\pi^{2}E}{\lambda^{2}}$

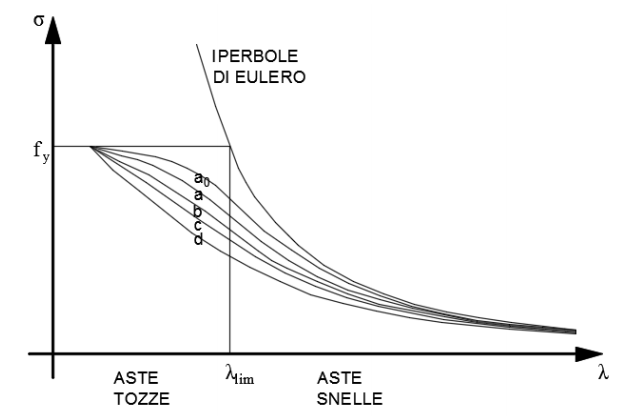
In cui λ è data dal rapporto tra la lunghezza libera di inflessione ed il raggio d’inerzia della sezione costituente l’asta ed è definita come snellezza. Un suo valore significativo è la snellezza limite λ_y, cioè quel valore che distingue le aste snelle da quelle tozze:

$\lambda_{y}=\pi\sqrt{\frac{E}{f_{y}}}$

λ < λ_yasta tozza
λ > λ_yasta snella

L’intersezione della snellezza limite con l’iperbole di Eulero individua, sull’asse verticale, il limite elastico f_y del materiale considerato.

Verifica di instabilità per i profili in acciaio

Secondo le NTC 2018 deve essere verificata la seguente disuguaglianza:

$\frac{N}{N_{b,Rd}}\leq1$

In cui N rappresenta lo sforzo di compressione agente e N_b,Rd la resistenza di progetto all’instabilità nell’asta compressa, data dalla seguente formula:

$N_{b,Rd}=\frac{\chi Af_{yk}}{\gamma M1}$

in cui:

A è l’area della sezione considerata;
f_yk è la resistenza del materiale costituente la sezione;
γ_M1 è il coefficiente di sicurezza del materiale;
χ è un coefficiente di riduzione che racchiude il fenomeno dell’instabilità; esso è valutato secondo la seguente formula:

$\chi=\frac{1}{\chi+\sqrt{\phi^{2}-\lambda^{2}}}\leq1$

$\phi=0,5\cdot[1+\alpha\cdot(\bar{\lambda^{2}}-0,2)+\bar{\lambda^{2}]}$

Si nota di come χ sia legato alla snellezza adimensionalizzata:

$\bar{\lambda}=\frac{\lambda}{\lambda_{y}}=\sqrt{\frac{Af_{yk}}{N_{cr}}}$

e al coefficiente di imperfezione α, a sua volta funzione della curva di instabilità per il profilo utilizzato:

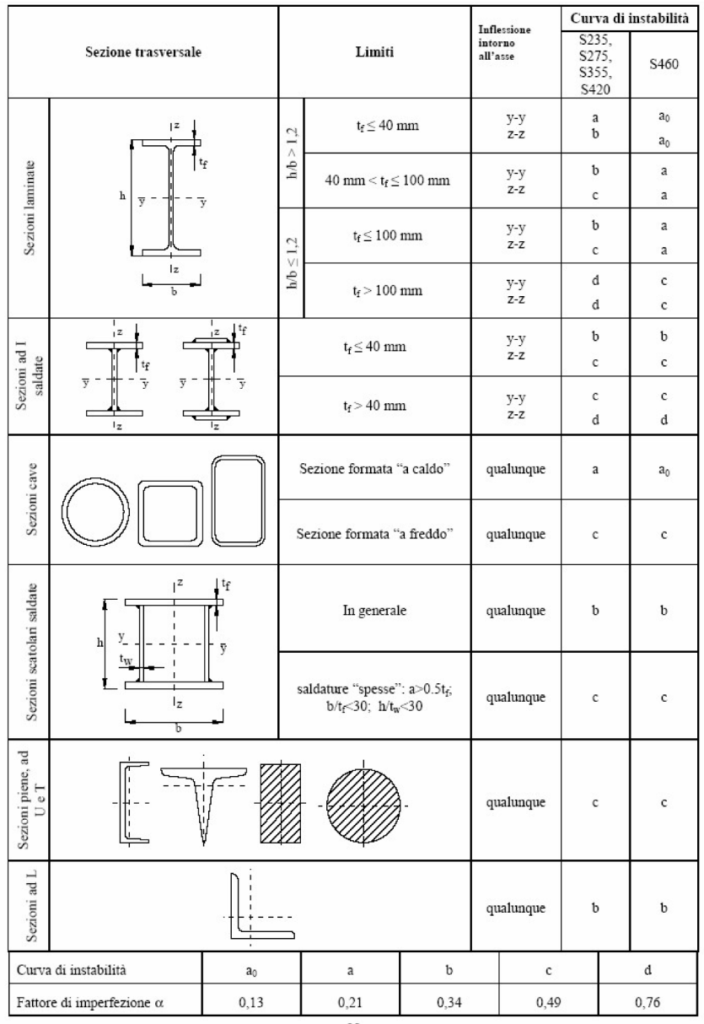
Effetti del secondo ordine

In alternativa, l’asta può essere verificata attraverso un’analisi degli effetti del secondo ordine legata alla presenza di imperfezioni alla freccia iniziale, funzione della pertinente curva d’instabilità, del metodo di analisi e del tipo di verifica della sezione trasversale.

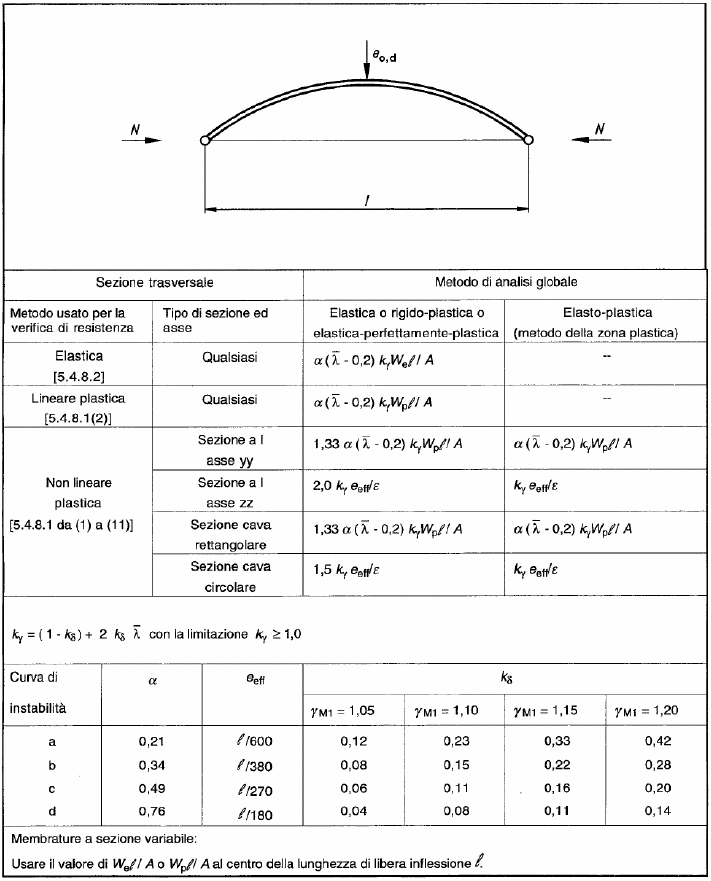
A titolo esemplificativo, si ipotizza di analizzare una struttura verificata e calcolata con metodo elastico e che presenti un valore di imperfezione iniziale e_0,d calcolato come:

$e_{0,d}=^{\alpha(\lambda^{*}-0,2)k_{\gamma}W_{el}}/A$

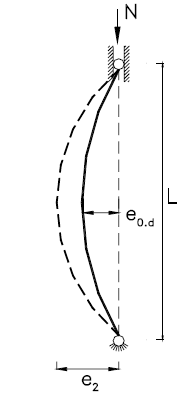
Supponendo una curva di instabilità a, per cui α = 0,21 k_δ = 0,23 e γ_M1 = 1,10, si ottiene:

$k_{\gamma}=(1-k_{\delta})+2k_{\delta}\bar{\lambda}\geq1,0$

L’amplificazione della freccia per effetto dell’imperfezione iniziale dell’asta, indicata con e₂, si calcola come:

$e_{2}=e_{0,d}/1-N/N_{cr}$

Dunque la verifica a pressione centrata con effetti del secondo ordine, equivale a una verifica a pressoflessione:

$f_{yd}\geq\frac{N}{A}+\frac{Ne_{2}}{W_{el}}$

Instabilità nel caso di pressoflessione

Osservando il comportamento di un’asta soggetta a un’imperfezione iniziale in mezzeria δ₀ e sottoposta a un carico N, Young formulò che il momento flettente massimo del secondo ordine a cui l’asta è soggetta è dato da:

$M_{2}=\frac{N\delta_{0}}{1-N/N_{cr}}$

Questa teoria fornisce un metodo di valutazione della freccia di inflessione in ipotesi di sforzo normale N e di imperfezione iniziale δ₀:

$\delta=\frac{\delta_{0}}{1-N/N_{cr}}$

Pertanto si può valutare il momento flettente del secondo ordine:

$M_{2}=M_{1}+N\delta=M_{1}+\frac{N\delta_{0}}{1-N/N_{cr}}=\frac{M_{1}}{1-N/N_{cr}}\left(1+\left(\frac{N_{cr}\delta_{0}}{M_{1}}-1\right)N/N_{cr}\right)$

Ponendo:

$\psi=\frac{N_{cr}\delta_{0}}{M_{1}}-1$

$N/N_{cr}=\theta$

Si ottiene:

$M_{2}=\frac{M_{1}\left(1+\psi\theta\right)}{1-\theta}=\frac{M_{eq}}{1-\theta}$

Poiché le NTC 2018 risultano di scarso contenuto per le verifiche di instabilità di un’asta pressoinflessa, è opportuno riferirsi all’Eurocodice 3, secondo cui:

$\frac{N}{N_{b,Rd}}+k\frac{M}{M_{c,Rd}}\leq1$

Con:

$k=1-\frac{\mu N}{\gamma_{M1}N_{b,Rd}}\leq1,5$

$\mu=\bar{\lambda}\left(2\beta_{m}-4\right)+\left(\frac{W_{pl}-W_{el}}{W_{el}}\right)\leq0,9$

Se, a vantaggio di sicurezza, si lavora in campo elastico utilizzando il W_el, la formula si trasforma in:

$\mu=\bar{\lambda}\left(2\beta_{m}-4\right)\leq0,9$

$M_{c,Rd}=M_{pl,Rd}$

$M_{c,Rd}=M_{el,Rd}$

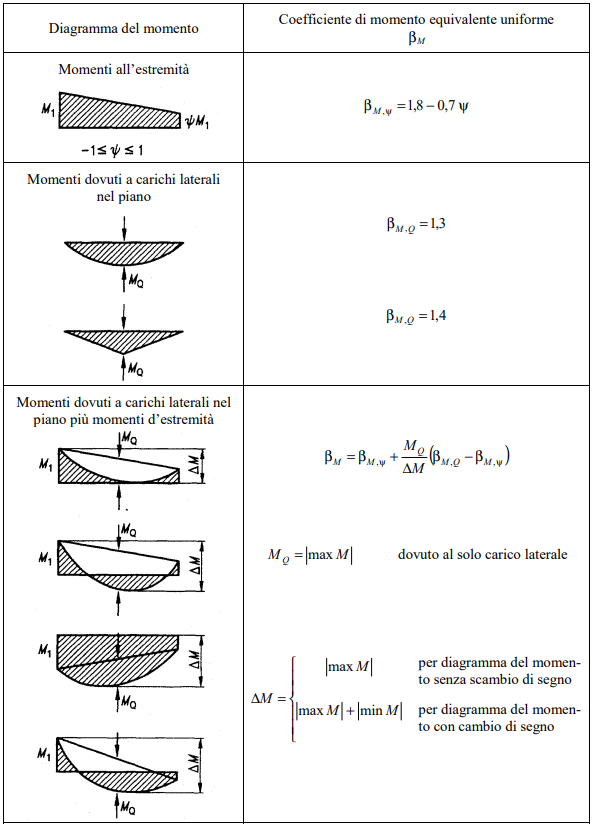
Il coefficiente di momento equivalente β_M consente di valutare la dipendenza μ alla distribuzione del momento lungo l’asta.

Il software che automatizza il calcolo della lunghezza libera di inflessione e del carico critico

A breve la soluzione innovativa di modellazione tridimensionale per il disegno esecutivo e il calcolo di tutti i ponteggi in acciaio: il nuovo Blumatica Ponteggi!

Senza sforzi e con pochi click potrai eseguire TUTTE le verifiche di resistenza e stabilità dei ponteggi completamente conformi alle prescrizioni NTC2018+Eurocodice3 e potrai stampare Pi.M.U.S., elaborati grafici e relazione di calcolo.

Compila questo form per essere avvisato sul rilascio e guadagnare uno sconto del 10%

blumatica carico critico

La redazione di calcolostrutturale.com è composta da ingegneri edili, copy strategist ed esperti di marketing e comunicazione.

Leggi tutti gli articoli di Redazione calcolostrutturale.com