Tali fenomeni possono compromettere la resistenza strutturale sia al livello delle intere membrature che al livello locale, quando la sezione retta delle travi è composta da elementi sottili, come quelle comunemente utilizzate per le strutture metalliche. Nonostante il relativamente alto valore della tensione ultima dei materiali da carpenteria metallica, la compressione che agisce nei piatti che compongono le travi con sezioni in parete sottile può facilmente determinare l’instabilità locale per valori di tensione relativamente bassi.

Tra le diverse strategie computazionali per l’analisi di travi con sezione in parete sottile, vanno certamente menzionati i metodi basati sulla modellazione dei singoli piatti che compongono la trave mediante una mesh molto fine di Elementi Finiti bidimensionali o tridimensionali, sicuramente più onerosi dal punto di vista computazionale Metodi alternativi sono, ad esempio, il Metodo delle Strisce Finite (FSM), che descrive i piatti che compongono la trave con sezione in parete sottile come un fascio di strisce parallele, o anche i metodi basati sulla Teoria Generalizzata della Trave (GBT), che descrive l’intera trave come un assemblaggio di piatti sottili la cui deformazione è descritta dalla combinazione lineare di un insieme di modi deformativi predefiniti.

Una risposta pragmatica, anche se approssimata,  alla necessità di tener conto dei fenomeni di instabilità locale nelle travi in parete sottile è quello suggerito dalle normative. Tanto le norme statunitensi che gli eurocodici (così come le norme italiane) adottano una classificazione dei piatti che compongono le sezioni in parete sottile in acciaio o alluminio al fine di determinare se la sezione sia in grado o meno di sviluppare una cerniera plastica prima che insorgano fenomeni di instabilità locale. In questo articolo descriverò un algoritmo per la classificazione automatica delle sezioni in parete sottile, con riferimento alle regole di classificazione definite dagli eurocodici.

L’instabilità locale delle travi con sezione in parete sottile

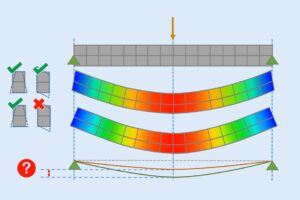
Per descrivere il fenomeno di instabilità che determina la perdita di resistenza dei piatti di una sezione in parete sottile, è utile esaminare l’esempio rappresentato nella Figura 1A, relativo a una trave compressa con sezione a I. I piatti che costituiscono la sezione subiscono un processo di imbozzamento e assumono una forma ondulata. Benché l’interazione tra i singoli piatti è un fenomeno complesso, è evidente che essi forniscono un vincolo parziale all’imbozzamento dei piatti a cui sono connessi.

Il fenomeno di imbozzamento può essere semplificato come la combinazione dell’imbozzamento dei singoli piatti che compongono la sezione, tenendo conto delle condizioni di vincolo che esprimono la connessione con i piatti adiacenti. Questo implica che l’instabilità influisce in modo diverso sui piatti dell’anima e quelli delle flange: a parità di dimensioni geometriche, le ali della sezione, avendo un lato libero, saranno soggette a instabilità per un valore di sforzo inferiore rispetto a quello che provoca l’instabilità del piatto d’anima, il quale è vincolato su tutto il perimetro.

Immaginando di esaminare separatamente ciascun piatto, è possibile osservare le configurazioni nelle Figure 1B, C e D. Nella Figura 1B, il piatto soggetto a compressione uniforme è vincolato solo alle estremità con un vincolo di appoggio semplice. Questo tipo di vincolo non si adatta a nessuno dei piatti nella sezione della trave della Figura 1A. In effetti, in questo caso, la forma della configurazione imbozzata è del tutto simile a quella di una trave soggetta a instabilità euleriana. La deformazione forma un’unica onda con una distanza tra i flessi corrispondente alla luce libera di inflessione L_o della trave, che è uguale alla luce della trave stessa. Per questo piatto, il carico critico sarà identico a quello euleriano e la distribuzione di tensioni normali lungo la larghezza del piatto sarà uniforme e pari alla tensione critica σ_cr.

Suppongo che il lettore conosca il fenomeno di instabilità euleriano o a carico di punta delle aste elastiche. Il valore dello sforzo normale che produce l’insorgere della instabilità di questi elementi strutturali dipende dal materiale di cui è composta l’asta, mediante il modulo elastico , e dalla geometria della trave e delle relative condizioni di vincolo, mediante la lunghezza libera di inflessione , e dell’inerzia  della sezione retta nella direzione lungo cui avvengono gli spostamenti che producono l’imbozzamento: . Va ricordato, comunque, che nella pratica progettuale si assume un valore dello sforzo normale critico diverso da quello teorico, poiché è necessario tener conto di imperfezioni geometriche e plasticità del materiale.

Nella Figura 1C, la piastra è vincolata su tre lati e, quando è soggetta a compressione, imbozza assumendo la forma rappresentata in figura, con una luce libera di inflessione ancora uguale alla lunghezza dell’intero piatto, ma con spostamenti trasversali crescenti man mano che ci si allontana dal vincolo laterale. Il comportamento di questa piastra è simile a quello dei piatti delle ali della trave con sezione ad I di Figura 1A. Date le diverse caratteristiche della configurazione imbozzata, è ragionevole aspettarsi che in questo caso il piatto abbia un carico critico superiore rispetto al caso della Figura 1B. A causa delle differenti condizioni di vincolo, la distribuzione di tensioni normali lungo la larghezza del piatto non è uniforme: l’instabilità provoca una significativa riduzione della tensione lungo il bordo libero; invece, lungo il bordo vincolato le tensioni possono raggiungere la tensione di snervamento σ_y del materiale, poiché le fibre longitudinali in questa zona non subiscono effetti significativi dall’instabilità. Questa distribuzione di tensioni normali può essere approssimata mediante una distribuzione uniforme di tensioni, agente su una larghezza ridotta b_eff del piatto.

Infine, quando la piastra è vincolata sull’intero perimetro (Figura 1D), similmente a come avviene anche per il piatto d’anima della trave con sezione ad I della Figura 1A, la forma della configurazione deformata è visibilmente diversa, caratterizzata generalmente da più onde. In questo caso, la distanza tra i flessi corrisponde a una lunghezza libera di inflessione che è dell’ordine di grandezza del lato corto della piastra. Di conseguenza, è ragionevole supporre che il carico critico sia maggiore rispetto a quello della piastra vincolata su tre lati. Analogamente al caso della Figura 1C, le fibre lungo i bordi vincolati subiscono in misura ridotta gli effetti dell’instabilità e sono in grado di raggiungere valori di tensione pari alla tensione di snervamento del materiale. Al contrario, le fibre nella zona centrale del piatto, dove gli spostamenti generati dall’instabilità sono più accentuati, possono sopportare valori di tensione notevolmente ridotti. Anche in questo caso, è possibile approssimare la reale distribuzione di tensioni immaginando che esse siano uniformi solo alle due estremità del piatto, per una larghezza ridotta pari a b_eff.

Benché questa descrizione semplificata renda l’idea di ciò che avviene sui piatti della sezione e giustifichi l’approccio normativo descritto di seguito, va ricordato che il fenomeno è più complesso di così, per diversi motivi. Innanzitutto, il fenomeno di instabilità non avviene quando il materiale ha comportamento elastico lineare, ma quasi sempre avviene in regime elastoplastico e per distribuzioni di tensioni certamente non coincidenti con quelli di compressione centrata. Inoltre, le condizioni di vicolo mutuo tra i piatti non è quella di semplice appoggio. Anzi, l’interazione tra i piatti fa sì che l’imbozzamento di un piatto possa influire sul modo in cui si deformano i piatti ad esse connessi. Ciò motiva l’utilizzo di approcci più raffinati come la modellazione fine delle sezioni in parete sottile o l’adozione di modelli avanzati quali i già citati FSM e GBT. La complessità del fenomeno, però, giustifica anche l’approccio normativo, basato su formulazioni estremamente semplificate, ma dalla semplice applicazione pratica. […]

Per leggere l’articolo completo acquista il numero 18 della rivista Lo Strutturista.

Per essere sempre aggiornato e leggere contenuti inediti abbonati alla rivista Lo Strutturista – La prima rivista per gli strutturisti italiani.