La ripartizione trasversale dei carichi nei ponti con impalcato a graticcio

Il problema, analizzato nel precedente articolo, della ripartizione dei carichi da traffico sulle travi longitudinali di un ponte a graticcio di travi si può risolvere, a mano, con tre metodi storici semplificati: il metodo di Courbon, il metodo di Engesser e quello di Guyon – Massonet – Bares.

Il metodo di Courbon e quello di Engesser partono dalle stesse ipotesi semplificative. Si considerano i traversi con un’infinita rigidezza flessionale e le travi longitudinali con rigidezza torsionale nulla.
L’ipotesi di traverso infinitamente rigido è stata valutata più volte sperimentalmente ed è dovuta, in parte, alla presenza della soletta d’impalcato.
In questo modo la soluzione che offrono i due metodi è facilmente riconducibile a quella di trave su suolo elastico, ricavando in maniera abbastanza semplice il coefficiente di ripartizione dei carichi (rij) in funzione del numero di travi e della posizione del carico sull’impalcato.

Metodo di Courbon

Il metodo di Courbon consiste nel considerare un numero infinito di traversi nell’impalcato del ponte a graticcio di travi. In questo modo sotto ogni posizione del carico (q(x)), supposto uniformemente distribuito lungo l’impalcato, si trova un traverso su cui grava un’aliquota di carico pari a (q(x)dx).
La distanza dx è considerata infinitesima.
In questo modo il traverso infinitamente rigido presente sotto ogni posizione del carico ripartisce l’aliquota di carico stesso sulle travi longitudinali in funzione del coefficiente di ripartizione determinato tramite la formula vista nell’articolo precedente e sotto riportata:

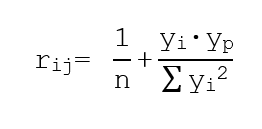
Metodo di Engesser

Il metodo di Engesser rimuove l’ipotesi di numero infinito di traversi e, a differenza del precedente, si basa sul principio di sovrapposizione degli effetti.
Tale metodo si sviluppa, di fatto, in tre fasi.

PRIMA FASE: si ipotizza un vincolo fittizio sotto ogni nodo tra la prima trave longitudinale dell’impalcato e ogni traverso che incrocia con essa. Si determinano, per questa configurazione statica, le sollecitazioni sulle travi longitudinali caricate e le reazioni dovute ai vincoli fittizi inseriti nel sistema.

SECONDA FASE: si rimuovono tutti i vincoli fittizi e si carica la prima trave longitudinale dell’impalcato con le reazioni determinate nella prima fase ricavando le sollecitazioni dovute a quest’ultime sulla trave longitudinale. Le reazioni vengono ripartite sulle altre travi longitudinali dell’impalcato da ponte tramite il coefficiente di ripartizione così definito:

TERZA FASE: si sovrappongono gli effetti delle sollecitazioni determinate nella prima e nella seconda fase.
Infine, si ripete la procedura sopra elencata per ogni trave longitudinale che costituisce l’impalcato da ponte.

Metodo di Guyon – Massonet – Bares

Il metodo di Guyon – Massonet – Bares diversamente degli altri due metodi si basa sulla definizione di una struttura equivalente continua e consiste nell’equiparare il graticcio di travi dell’impalcato da ponte ad una piastra ortotropa di cui si conosce la soluzione in forma chiusa. In questo modo si rende il metodo facilmente tabellabile con risultati di pronto utilizzo per il progettista.